2) Так как не дано никаких ограничений по значению переменной , то можно сказать, что наибольшего значения это выражение достигает при наибольшем косинусе, а наибольший возможный косинус равен 1. Такое возможно, если . Таким образом, наибольшее значение данного выражения равно .
ответ: 4
Пошаговое решение:
1) Упростим выражение.
2) Так как не дано никаких ограничений по значению переменной , то можно сказать, что наибольшего значения это выражение достигает при наибольшем косинусе, а наибольший возможный косинус равен 1. Такое возможно, если
, то можно сказать, что наибольшего значения это выражение достигает при наибольшем косинусе, а наибольший возможный косинус равен 1. Такое возможно, если 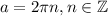 . Таким образом, наибольшее значение данного выражения равно
. Таким образом, наибольшее значение данного выражения равно 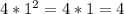 .
.