На самом деле задача примитивна и, судя по виду, придумана для учеников 7-ых классов. Действительно, здесь мы видим две простейшие формулы сокращенного умножения.
В числителе - это:
А в знаменателе наблюдается:
Данные формулу очень удобны, что демонстрирует данный пример. Однако важно заметить их неединственность. Необходимо изучить все, чтобы быть готовым к любы аналогичным заданиям.
(см. объяснение)
Объяснение:
Рассмотрим числитель дроби:
Рассмотрим знаменатель дроби:
Тогда ответом будет число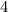 .
.
Задание выполнено!
Комментарий:
На самом деле задача примитивна и, судя по виду, придумана для учеников 7-ых классов. Действительно, здесь мы видим две простейшие формулы сокращенного умножения.
В числителе - это:
А в знаменателе наблюдается: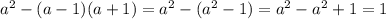
Данные формулу очень удобны, что демонстрирует данный пример. Однако важно заметить их неединственность. Необходимо изучить все, чтобы быть готовым к любы аналогичным заданиям.
2sin^2x-7cos2x=6sin2x+7
Разложим в левой и правой частях уравнения косинус и синус двойного угла
2sin^2x-7(cos^2x-sin^2x)=12sinxcosx+7
Представим sin^2x в скобках через основное тригонометрическое тождество
2sin^2x-7(cos^2x-(1-cos^2x))=12sinxcosx+7
Раскроем скобки
2sin^2x-7(2cos^2x-1)=12sinxcosx+7
2sin^2x-14cos^2x+7=12sinxcosx+7
Перенесем 7 влево и разделим обе части на cos^2x
2tg^2x-14=12tgx
Замена tgx=t
2t^2-14-12t=0
Разделим обе части на 2
t^2-7-6t=0
По теореме Виетта решим квадратное уравнение
t1*t2=-7
t1+t2=6
Отсюда следует, что t1=7, t2=-1
tgx=t1
х1=arctg7+Пn
tgx=t2
х=arctg1+Пn
x2=П/4+Пn