При производная неотрицательна, значит, на данном промежутке функция возрастает.
При производная отрицательна, значит, на данном промежутке функция убывает.
Таким образом, точка минимума функции — x = 1. На отрезке [0; 3] функция принимает наименьшее значение именно в этой точке. Значит, наименьшее значение функции на заданном промежутке .
Найдём нули производной:
При![x\in(-\infty;-1]\cup [1;+\infty)](/tpl/images/0468/1994/d626f.png) производная неотрицательна, значит, на данном промежутке функция возрастает.
производная неотрицательна, значит, на данном промежутке функция возрастает.
При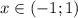 производная отрицательна, значит, на данном промежутке функция убывает.
производная отрицательна, значит, на данном промежутке функция убывает.
Таким образом, точка минимума функции — x = 1. На отрезке [0; 3] функция принимает наименьшее значение именно в этой точке. Значит, наименьшее значение функции на заданном промежутке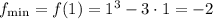 .
.
ответ: -2