Наименьшее значение функции - 13.2501054 или ln(0.5)^-5 + 19.5 в точке x = 3.5.
Объяснение:
Функция принимает своё максимальное(минимальное) значение тогда, когда производная функции равна 0.
f'(x) = + 5 = 0
Корней нет, найдём значение функции на краях отрезка
При x = 3.5
f(3.5) = ln(0.5)^-5 + 5*3.5 + 2 ≈ 13.2501054 - локальный минимум
f(7) = ln(4)^-5 + 35 + 2 ≈ 37.1953092 - локальный максимум
Наименьшее значение функции - 13.2501054 или ln(0.5)^-5 + 19.5 в точке x = 3.5.
Объяснение:
Функция принимает своё максимальное(минимальное) значение тогда, когда производная функции равна 0.
f'(x) =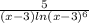 + 5 = 0
+ 5 = 0
Корней нет, найдём значение функции на краях отрезка
При x = 3.5
f(3.5) = ln(0.5)^-5 + 5*3.5 + 2 ≈ 13.2501054 - локальный минимум
f(7) = ln(4)^-5 + 35 + 2 ≈ 37.1953092 - локальный максимум
Наименьшее значение функции - 13.2501054 или ln(0.5)^-5 + 19.5 в точке x = 3.5.