1. Производная функции:
2. y' = 0;
Это уравнение решений не имеет, т.к. косинус изменяется от -1 до 1.
3. Найдем наименьшее значение функции на концах отрезка.
- min
ответ:
1. Производная функции:
2. y' = 0;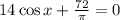
Это уравнение решений не имеет, т.к. косинус изменяется от -1 до 1.
3. Найдем наименьшее значение функции на концах отрезка.
ответ:![\displaystyle \min_\big{\left[-\frac{5\pi}{6};0\right]}y(x)=y\left(-\frac{5\pi}{6}\right)=-41](/tpl/images/0345/4861/4dd09.png)