-9
Объяснение:
Перепишем функцию, как
, для любых x, т.к. дискриминант квадратичной формы меньше 0
Равно 0 только при y=0.
Функция достигает минимума при x=3, минимальное значение -9
Значит наименьшее значение функция достигает в точке (3,0) и оно равно 0-9=-9
-9
Объяснение:
Перепишем функцию, как
Равно 0 только при y=0.
Функция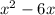 достигает минимума при x=3, минимальное значение -9
достигает минимума при x=3, минимальное значение -9
Значит наименьшее значение функция достигает в точке (3,0) и оно равно 0-9=-9