0
Объяснение:
Найдём экстремумы функции :
Найдем производную:
Найдем корни уравнения
То есть в точке 0 функция имеет глобальный минимум.
Так как функция в точке 0 имеет глобальный минимум:
, а точка 0 находится между точками -1 и 2, то
0
Объяснение:
Найдём экстремумы функции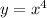 :
:
Найдем производную: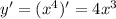
Найдем корни уравнения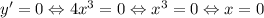
То есть в точке 0 функция имеет глобальный минимум.
Так как функция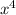 в точке 0 имеет глобальный минимум:
в точке 0 имеет глобальный минимум: