Найдите объем фигуры, образованной вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции у = х^3, касательной к этому графику в точке с абсциссой х0 = 1 и прямой у = 0.
8) Высота, проведённая из вершины прямого угла к гипотенузе является средним пропорциональным между отрезками, на которые делится гипотенуза основанием высоты, то есть h²=a*b, где а=18, b=32
h²=576, h=24
Гипотенуза с=a+b=18+32=50
Площадь S=1/2*h*c=1/2*24*50=600
6) a₁=4, d=3 S(n)=246
S(n)=[ (2a₁+d(n-1)) /2 ]*n
2*4+3n-3
S(n)= * n =246
2
3n²+5n-492=0 , D=25+4*3*492=5929 , √D=77 ,
n₁=(-5-77)/6=-82/6=-41/3
n₂=(-5+77)/6=72/6=12
Надо взять первых 12 членов прогрессии, чтобы получить S=246
5) Чтобы построить график, надо определить несколько характерных точек для кривой и провести через них кривую.
Заданная ф-ция - парабола.Так как перед х² коэффициент равен (-1), то ветви параболы направлены вниз. Поэтому наибольшее значение ф-ция принимает в вершине.
Точки пересечения с осью ОХ: 3+2х-х²=0 ⇒ х²-2х-3=0
По теореме Виета х₁=-1 , х₂=3 ⇒ точки А(-1,0) и В(3,0) пересечения с ОХ.
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2)
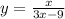. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)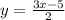
при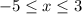 
Если x = -5, то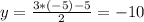
Если х= 3, то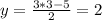
Значит,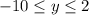
8) Высота, проведённая из вершины прямого угла к гипотенузе является средним пропорциональным между отрезками, на которые делится гипотенуза основанием высоты, то есть h²=a*b, где а=18, b=32
h²=576, h=24
Гипотенуза с=a+b=18+32=50
Площадь S=1/2*h*c=1/2*24*50=600
6) a₁=4, d=3 S(n)=246
S(n)=[ (2a₁+d(n-1)) /2 ]*n
2*4+3n-3
S(n)= * n =246
2
3n²+5n-492=0 , D=25+4*3*492=5929 , √D=77 ,
n₁=(-5-77)/6=-82/6=-41/3
n₂=(-5+77)/6=72/6=12
Надо взять первых 12 членов прогрессии, чтобы получить S=246
5) Чтобы построить график, надо определить несколько характерных точек для кривой и провести через них кривую.
Заданная ф-ция - парабола.Так как перед х² коэффициент равен (-1), то ветви параболы направлены вниз. Поэтому наибольшее значение ф-ция принимает в вершине.
Точки пересечения с осью ОХ: 3+2х-х²=0 ⇒ х²-2х-3=0
По теореме Виета х₁=-1 , х₂=3 ⇒ точки А(-1,0) и В(3,0) пересечения с ОХ.
Вершина параболы: х(верш)=-b/2a=-2/-2=1 , y(верш)=3+2*1-1²=3+2-1=4
Точка С(1,4) - вершина параболы. ⇒ Наибольшее значение ф-ция у=3+2х-х² - это число 4,значит множество значений ф-ции Е(у)=(-∞,4].
Промежуток убывания - (1,+∞).