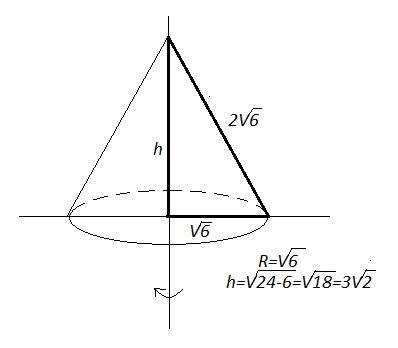
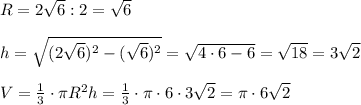Найдите объем конуса,полученного вращением равностороннего треугольника со стороной 2√6 вокруг своей высоты с полным решением и ответом ! это удвоенный объем конуса, у которого высота равна v6 ( 2v6 : 2= v6) v - значок корня ( катет в два раза меньше гипотенузы, лежащей против угла в 30 гр) образующая конуса 2v6 - это из условия основание конуса - окружнисть с радиусом, который вычисляем по теореме пифагора r^2 = (2v6)^2 -( v6)^2 r = 3v2 радиус знаем, значит найдем площадь основания конуса s = pi*r^2 а объем считаем по формуле h/3 * s только у нас два таких конуса, значит два объема 2h/3 * s высоту знаем, площадь посчитаем . вот цифры подставьте и посчитайте.