1) Допустим, было граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было .
Составляем уравнение:
5% · + 10% · = 8% · 60;
Тогда 5%-ого раствора было 24 г, а 10% - 60 - 24 = 36 (г).
ОТВЕТ: 5%-ого - 24 г, 10%-ого - 36 г.
2) Допусти, у нас есть "десятирублевок". Тогда "пятирублевок" всего .
Десятирублевых монет - 7. Пятирублевых - 25 - 7 = 18
ОТВЕТ: десятирублевых - 7; пятирублевых - 18.
3) Пусть вагон весит т. Тогда электровоз стоит .
Один вагон весит 16,8 т. Тогда электровоз весит 5 · 16,8 + 6,5 = 90,5 (т).
ОТВЕТ: вагон весит 16,8 т, электровоз - 90,5 т.
При делении степеней с одинаковыми основаниями основание оставляют прежним а из показателя числителя вычитают показатель знаменателя
При возведении степени в степень основания оставляют прежним , а показатели перемножают
При возведении в степень произведения возводят в эту степень множители и результаты перемножают
Степень числа а (а≠0) с нулевым показателем равна 1
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равен а
Степень числа а с показателем равным 1 равна самому числу а
При умножении степеней с одинаковыми основаниями показатели складывают, а основание оставляют прежним
1) Допустим, было граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было
граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было  .
.
Составляем уравнение:
5% · + 10% ·
+ 10% · 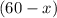 = 8% · 60;
= 8% · 60;
Тогда 5%-ого раствора было 24 г, а 10% - 60 - 24 = 36 (г).
ОТВЕТ: 5%-ого - 24 г, 10%-ого - 36 г.
2) Допусти, у нас есть "десятирублевок". Тогда "пятирублевок" всего
"десятирублевок". Тогда "пятирублевок" всего  .
.
Составляем уравнение:
Десятирублевых монет - 7. Пятирублевых - 25 - 7 = 18
ОТВЕТ: десятирублевых - 7; пятирублевых - 18.
3) Пусть вагон весит т. Тогда электровоз стоит
т. Тогда электровоз стоит 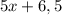 .
.
Составляем уравнение:
Один вагон весит 16,8 т. Тогда электровоз весит 5 · 16,8 + 6,5 = 90,5 (т).
ОТВЕТ: вагон весит 16,8 т, электровоз - 90,5 т.
При делении степеней с одинаковыми основаниями основание оставляют прежним а из показателя числителя вычитают показатель знаменателя
При возведении степени в степень основания оставляют прежним , а показатели перемножают
При возведении в степень произведения возводят в эту степень множители и результаты перемножают
Степень числа а (а≠0) с нулевым показателем равна 1
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равен а
Степень числа а с показателем равным 1 равна самому числу а
При умножении степеней с одинаковыми основаниями показатели складывают, а основание оставляют прежним