Решаем получившееся неравенство:
Решим методом интервалов:
нули числителя: 0
нули знаменателя: 1
- + -
-------------------------о-------------------------о---------------------> x
0 1
Так как нам нужны промежутки, где выражение имеет положительное значение, то областью определения данной функции является: .
Решаем получившееся неравенство:
Решим методом интервалов:
нули числителя: 0
нули знаменателя: 1
- + -
-------------------------о-------------------------о---------------------> x
0 1
Так как нам нужны промежутки, где выражение имеет положительное значение, то областью определения данной функции является: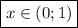 .
.