Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая: .
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
Линейная функция задаётся уравнением .
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
Округлить до десятков:
75≈80; 34≈30; 816≈820; 42≈40; 1859≈1860; 6394≈6400.
Округлить до сотен:
612≈700
871≈900
1304≈13 00
1950≈2000
округлить до тысяч
5402≈5000
27834≈28000
30456≈30000
34567≈35000
Округлить до десяти тысяч:
6009842≈6010000
15624035≈15620000
34567≈30000
Округлить до целых:
77,57≈78
124,1≈124
16,027≈16
421,87≈422
3,94≈4
Округлить до десятых:
657,239≈657,2
0,512≈0,5
57,429≈57,4
99,98≈100
Округлить до сотых:
0,07612≈0,08
8,571≈8,58
13,042≈13,04
1,9507≈1,95
Округлить до тысячных:
8,32715≈8,327
49,0562≈49,056
748,0998≈748,1
ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая: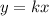 .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
Линейная функция задаётся уравнением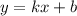 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид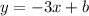
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.