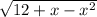Объяснение:
Приравняем к нулю
Решим по методы интервалов:
(фото в верху)
x∈(-3;4) область определение
Объяснение:
Приравняем к нулю
Решим по методы интервалов:
(фото в верху)
Объяснение:
x∈(-3;4) область определение