Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
hshdk
01.12.2022 10:11 •
Алгебра
Найдите общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием y=y0 при x=x0 ydx=(x+1)dy. y(0)=1
Показать ответ
Ответ:
vhovalyg90
11.06.2021 09:09
- общее решение
Используем условие
:
- частное решение
0,0
(0 оценок)
Популярные вопросы: Алгебра
maksimesaulav46
20.07.2022 22:24
Разложи на множители 2xy−14x−6y+42....
AlisaSkun3
26.11.2021 04:11
Найти общее решение: y -2y -3y=...
vlad1417
14.03.2020 10:00
Назови коэффициенты a, b и c линейного уравнения с двумя переменными: x-2y+3=0 a= b= c=...
Gusein123
18.03.2020 00:31
найти значение выражения с корнями, 9 класс...
ПУТИН222
03.01.2023 18:38
1) Число 4 є коренем рівняння x2+ax-24=0.Знайдіть значення а і другий корінь рівняння (розписати) 2) Число -1/5 є коренем рівняння 10x2+kx-7=0.Знайдіть значення К і другий корінь...
ruslan5632
26.07.2022 14:11
Полусумма чисел x и 5 равна их произведению...
sveta05011
19.02.2020 23:10
два стрелка по 30 выстрелов каждый. На мишени обнаружено 40 пробоин.Сколько раз попал каждый ,если известно, что у первого стрелка на один неудачный выстрел приходилось в 5 раз больше...
garvarrd
09.06.2021 00:31
Укажите промежутки на которых функция имеет положительные значения...
dfrt2
02.04.2020 06:15
На координатной плоскости изобразите штриховкой решение неравенсва: у≥ х2 - 3 (ЧЕРТЕЖ И РЕШЕНИЕ...
fox359
18.02.2022 00:16
ПОДРОБНОЕ РЕШЕНИЕ ПОЖАЙЛУСТА...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Используем условие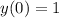 :
: