Найдите первообразные функции
1 вариант 2 вариант
ƒ(x)= 3/cos^2 x ƒ(x) = 4/sin^2 x
ƒ(x) = -7sinx ƒ(x) =1,2cosx
ƒ(x) = sinx – cosx ƒ (x) = 2sin (π/2-x)
ƒ(x) = 2sinx - 1/cos^2 x ƒ(x)= 21/(〖cos〗^2 x) - 1/sin^2 x
Решите задачу
1 вариант
Найдите значение первообразной функции ƒ(x) =2/cos^2 (3x+π/4)) при x = π/4 , график которой проходит через данную точку M(0;12/3)
2 вариант
Найдите значение первообразной функции ƒ(x) =2/(〖cos〗^2 (π/4-x)) при x = π/12, график которой проходит через данную точку M (- 3π/4 ;3).
Вычислите неопределенные интегралы:
∫▒〖x^4 dx〗
∫▒〖5x^7 dx〗
∫▒x^3 (x^2-1)dx
∫▒(af+d)dx
∫▒〖(7-3t-t^3 〗)dt
∫▒〖(〖24u〗^3 〗-54u^2- 74u-3)du
∫▒dx/√(25-x^2 )
∫▒dx/(5-〖2x〗^2 )
∫▒〖(3x-1)^5 〗 dx
∫▒〖(1+4x)^(3/5) 〗 dx
∫▒xdx/(x^3- 1)
∫▒dx/(x^4-1)
∫▒(x^8-〖3x〗^5-x+1)/x^3 dx
∫▒((x+1)(x^2-3))/〖3x〗^2 dx
∫▒1/x^2 x^(1/2) dx
∫▒〖sinx〖cos〗^7 xdx〗
∫▒〖(〖ax〗^7 〗+〖6x〗^3+〖cx〗^2+dx+l√x+f)dx
∫▒〖(√t〗-1/√t)dx
∫▒〖2^x+〗 3^2x+5^3x dx
В первом уравнении мы раскрыли модуль: при x > 0 уравнение имеет вид y + a = 1, при x ≤ 0 оно не определено.
График первого уравнения - прямая, параллельная оси Ox, которая определена при x > 0. График второго уравнения - парабола, её вершина имеет координаты (-a; -3). При движении прямой вниз парабола сдвигается влево, а при движении прямой вверх - вправо.
Система имеет одно решение, если прямая касается параболы или парабола пересекает её один раз.
1 случай. Касание. Прямая, которая касается параболы, имеет уравнение y = -3 ⇒ 1 - a = -3 ⇔ a = 4. Но тогда вершина параболы будет иметь координату (-4; -3), а при x < 0 первое уравнение не определено. a = 4 не подходит.
2 случай. Пересечение. Если бы прямая y = 1 - a была определена в точке x = 0, то парабола имела бы одно пересечение с прямой в некой точке (0; y₁), двигалась вправо, пока её левая ветвь вновь не пересекла прямую в точке (0; y₂). Но x = 0 не входит в область определения, поэтому это лишь меняет границы полуинтервала местами (т. е. если левая граница была исключена, а правая включена, то сейчас наоборот: левая включена, правая исключена). Подставим координаты (0; y) и составим уравнение:
Правая граница исключается, иначе не будет пересечений, левая включается, т. к. при таком a всё ещё будет одно пересечение.
ответ: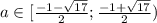
Решаем две системы
решение системы предполагает рассмотрение двух случаев
а) при (5х-9)>1 логарифмическая функция возрастает, большему значению аргумента соответствует большее значение функции и с учетом, того что под знаком логарифма выражение должно быть строго положительным, получаем систему четырех неравенств:
20-11х≥0;
5x-9>1;
х²-4х+5≤1;
х²-4х+5>0.
Решение каждого неравенства системы:
х≤20/11
х>1,8
х=2
х- любое
О т в е т. 1а) система не имеет решений.
б) при 0<(5х-9)<1 логарифмическая функция убывает, большему значению аргумента соответствует меньшее значение функции и с учетом, того что под знаком логарифма выражение должно быть строго положительным, получаем систему четырех неравенств:
20-11х≥0
0<5x-9<1
х²-4х+5≥1
х²-4х+5>0
Решение
х≤20/11
0<х<1,8
х-любое (так как х²-4х+4≥0 при любом х)
х- любое
Решение системы 1б) 0<x<1,8, так как (20/11) >1,8
О т в е т. 1)0<x<1,8
решение системы также предполагает рассмотрение двух случаев
а) при (5х-9)>1 логарифмическая функция возрастает, большему значению аргумента соответствует большее значение функции и с учетом, того что под знаком логарифма выражение должно быть строго положительным, получаем систему четырех неравенств:
20-11х≤0
5x-9>1
х²-4х+5≥1
х²-4х+5>0
Решение
х≥20/11
х>1,8
х-любое
х- любое
О т в е т. 2 а) х≥20/11.
б) при 0<(5х-9)<1 логарифмическая функция убывает, большему значению аргумента соответствует меньшее значение функции и с учетом, того что под знаком логарифма выражение должно быть строго положительным, получаем систему четырех неравенств:
20-11х≤0
0<5x-9<1
х²-4х+5≤1
х²-4х+5>0
Решение
х≥20/11
0<х<1,8
х=2
х- любое
Решение системы 2б) нет решений
О т в е т. 2) х≥20/11
О т в е т. 0 < x < 1,8 ; x≥20/11
или х∈(0;1,8)U(1целая 9/11;+∞)