Найдите подходящее правило и заполните многоточия в соответствии с ним 4-2, 7-1, 12-3, 27-3, 21-5, 15-2, 16-4, 32-5, 101-1 31- , 8- , 125- , 128- , 144- , 72-
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
При х=0 функция имеет разрыв 1 рода .
При х=2 функция непрерывна.
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
На 1 рисунке нет чертежа функции при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
Объяснение:[
3
−
4
−
5
7
]
Матрица обратная к матрице
2
×
2
, может быть найдена по формуле
1
|
A
|
[
d
−
b
−
c
a
]
, где
|
A
|
это определитель
A
.
Если
A
=
[
a
b
c
d
]
, то
A
−
1
=
1
|
A
|
[
d
−
b
−
c
a
]
Определитель
[
3
−
4
−
5
7
]
равен
1
.
Нажмите, чтобы увидеть больше шагов...
1
Подставим известные значения в формулу обратной матрицы.
1
1
[
7
−
(
−
4
)
−
(
−
5
)
3
]
Упростим каждый элемент матрицы
[
7
−
(
−
4
)
−
(
−
5
)
3
]
.
Нажмите, чтобы увидеть больше шагов...
1
1
[
7
4
5
3
]
Умножим
1
1
на каждый элемент матрицы.
[
1
1
⋅
7
1
1
⋅
4
1
1
⋅
5
1
1
⋅
3
]
Упростим каждый элемент матрицы
[
1
1
⋅
7
1
1
⋅
4
1
1
⋅
5
1
1
⋅
3
]
.
Нажмите, чтобы увидеть больше шагов...
[
7
4
5
3
]
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
При х=0 функция имеет разрыв 1 рода .
При х=2 функция непрерывна.
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
На 1 рисунке нет чертежа функции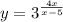
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .