Проведем отрезки OB и OC, как показано на рисунке. Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои хорды пополам (по свойству хорды) Получается, что треугольники OEB и OCF - прямоугольные, EB=AB/2 и CF=CD/2. По теореме Пифагора: OB2=OE2+EB2 OB2=242+(20/2)2 OB2=576+100=676 OB=26 OB=OC=26 (т.к. OB и OC - радиусы окружности) По теореме Пифагора: OC2=CF2+FO2 OC2=(CD/2)2+FO2 262=(CD/2)2+102 676=(CD/2)2+100 (CD/2)2=576 CD/2=24 CD=48 ответ: CD=48
Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои хорды пополам (по свойству хорды)
Получается, что треугольники OEB и OCF - прямоугольные, EB=AB/2 и CF=CD/2.
По теореме Пифагора:
OB2=OE2+EB2
OB2=242+(20/2)2
OB2=576+100=676
OB=26
OB=OC=26 (т.к. OB и OC - радиусы окружности)
По теореме Пифагора:
OC2=CF2+FO2
OC2=(CD/2)2+FO2
262=(CD/2)2+102
676=(CD/2)2+100
(CD/2)2=576
CD/2=24
CD=48
ответ: CD=48
1. Обратно пропорциональная зависимость :
2. Решите графически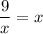
График функции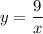 - гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение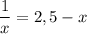
График функции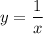 - гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.