Решим нашу симметрическую систему. Многие пытаются решать подстановки, выразив одну переменную через другую. Так можно делать. Но я покажу значительно более изящный и красивый решения таких систем. Прежде всего, введём замену. Пусть x + y = a, xy = b. очевидность этой замены станет ясна чуть позже. Теперь рассмотрим x^2 + y^2. Заметим, что x^2 + y^2 = (x+y)^2 - 2xy = a^2 - 2b Последний шаг очевиден, поскольку я просто подставил наши новые переменные. Теперь получаем систему уравнений с дувмя переменными. a = 3 a = 3 a^2-2b = 29 2b = a^2 - 29 = 9 - 29 = -20 Откуда b = -10. Теперь, учитывая, что a = 3, b = -10, получим ещё одну систему уравнений относительно x и y: x + y = 3 xy = -10 Решается система элементарно, с подстановки: y = 3 - x 3x - x^2 = -10 x^2 - 3x - 10 = 0 x(3-x) = -10 y = 3 - x y = 3-x Из теоремы Виета следует, что возможны два случая: x1 = 5; x2 = -2 Отсюда в двух случаях находим y и записываем ответ: y1 = 3 - 5 = -2 y2 = 3 + 2 = 5 ответ:(5;-2); (-2;5) Кстати, обратите внимание на ответ. Обе пары как бы симметричны друг другу.
Пусть х — количество учеников, которые были в комнатах по 4 человека. Тогда х/4 — количество четырёхместных комнат (х учеников расселили в комнаты по 4 человека). Количество человек, живших в трёхместных комнатах — 71-х (т. к. все, кто не жил в четырёхместных комнатах, жили в трёхместных). Тогда количество трёхместных комнат — (71-х)/3 (71-х человек расселили в комнаты по трое). Так как всего комнат 20, и они были только трёхместные и четырёхместные, получаем:
20= (20 комнат — это все комнаты, и трёхместные, и четырёхместные).
Решим получившееся уравнение:
20=
20 =
20=
Умножим обе части на 12:
240 = 284 - х
х = 284 - 240
х = 44
ответ: 44.
Примечание: чтобы убедиться в правильности ответа, можно сделать проверку:
Если в комнатах по 4 человека жили 44 ученика, всего четырёхместных комнат было 44/4=11.
Т. к. всего комнат 20, то трёхместрых комнат 20-11=9 комнат. Т. к. все они заполнены, в них должно жить 9*3=27 учеников.
После того, как 44 ученика поселили в четырёхместные комнаты, осталось 71-44=27 детей — именно столько должно было жить в трёхместных комнатах.
Прежде всего, введём замену.
Пусть x + y = a, xy = b. очевидность этой замены станет ясна чуть позже.
Теперь рассмотрим x^2 + y^2. Заметим, что x^2 + y^2 = (x+y)^2 - 2xy = a^2 - 2b
Последний шаг очевиден, поскольку я просто подставил наши новые переменные.
Теперь получаем систему уравнений с дувмя переменными.
a = 3 a = 3
a^2-2b = 29 2b = a^2 - 29 = 9 - 29 = -20
Откуда b = -10.
Теперь, учитывая, что a = 3, b = -10, получим ещё одну систему уравнений относительно x и y:
x + y = 3
xy = -10
Решается система элементарно, с подстановки:
y = 3 - x 3x - x^2 = -10 x^2 - 3x - 10 = 0
x(3-x) = -10 y = 3 - x y = 3-x
Из теоремы Виета следует, что возможны два случая:
x1 = 5; x2 = -2
Отсюда в двух случаях находим y и записываем ответ:
y1 = 3 - 5 = -2 y2 = 3 + 2 = 5
ответ:(5;-2); (-2;5)
Кстати, обратите внимание на ответ. Обе пары как бы симметричны друг другу.
ответ: 44
Объяснение:
Пусть х — количество учеников, которые были в комнатах по 4 человека. Тогда х/4 — количество четырёхместных комнат (х учеников расселили в комнаты по 4 человека). Количество человек, живших в трёхместных комнатах — 71-х (т. к. все, кто не жил в четырёхместных комнатах, жили в трёхместных). Тогда количество трёхместных комнат — (71-х)/3 (71-х человек расселили в комнаты по трое). Так как всего комнат 20, и они были только трёхместные и четырёхместные, получаем:
20=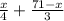
(20 комнат — это все комнаты, и трёхместные, и четырёхместные).
Решим получившееся уравнение:
20=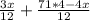
20 =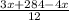
20=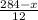
Умножим обе части на 12:
240 = 284 - х
х = 284 - 240
х = 44
ответ: 44.
Примечание: чтобы убедиться в правильности ответа, можно сделать проверку:
Если в комнатах по 4 человека жили 44 ученика, всего четырёхместных комнат было 44/4=11.
Т. к. всего комнат 20, то трёхместрых комнат 20-11=9 комнат. Т. к. все они заполнены, в них должно жить 9*3=27 учеников.
После того, как 44 ученика поселили в четырёхместные комнаты, осталось 71-44=27 детей — именно столько должно было жить в трёхместных комнатах.
Проверка показала, что найденный ответ верен.