5)
Объяснение:
так как 0<28<90 - то косинус положителен
sin236=sin(180+56)=-sin56, ( формула: sin2a=2sina*cosa) =
-2sin28*cos28=-2*a*cos28= (формула: cos^2a=1-sin^2a) =
-2*a*V(1-a^2), (1-a^2 стоит под корнем V )
5)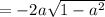
Объяснение:
так как 0<28<90 - то косинус положителен
Объяснение:
sin236=sin(180+56)=-sin56, ( формула: sin2a=2sina*cosa) =
-2sin28*cos28=-2*a*cos28= (формула: cos^2a=1-sin^2a) =
-2*a*V(1-a^2), (1-a^2 стоит под корнем V )