Найдите среднее арифметическое ряда чисел, его моду и размах: 13; 15; 13; 12; 12; 12; 13; 14; 13; 15; 13; 12; 12. 1) составьте для этих статистических данных вариационный ряд. 2) найдите абсолютную и относительную частоту для значений варианты, входящий в этот ряд. 3) представьте результаты выборки в виде полигона частот. , все , !
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
Рассмотрим функцию![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png) . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
Если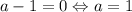 , то это линейное уравнение, имеющее не более одного корня, что не подходит.
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если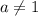 , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
Учитывая, что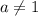 , получаем ответ
, получаем ответ 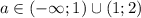
Объяснение:
Нам необходимо доказать, что
S(n) = 1 / 1 * 2 + 1 /2 * 3 + ... + 1 /n * (n + 1) = n / (n + 1).
Проведем доказательство по индукции.
S(1) = 1 / 1 * 2 = 1/2 = 1 /(1 + 1) = 1/2.
Предположим, что утверждение верно
для любого натурального к <= n.
Тогда
S(n + 1) = 1 / 1 * 2 + 1 / 2 * 3 + ... + 1 / n * (n + 1) +
+ 1 / (n + 1) * (n + 2) = S(n) + 1 / (n + 1) * (n + 2) =
= n / (n + 1) + 1 / (n + 1) * (n + 2) =
= (n * (n + 2) + 1) / (n + 1) * (n + 2) =
= (n^2 + 2 * n + 1) / (n + 1) * (n + 2) =
= (n + 1)^2 / (n + 1) * (n + 2) = (n + 1) / (n + 2)