Найдите стороны равнобедренного треугольника, если боковая сторона треугольника делится точкой касания вписанной окружности в отношении 4:5,считая от вершины угла при основании треугольника, а его периметр 104 cм.

Показать ответ

Ответ:

hardrop

29.10.2020 07:22

у=7х

Объяснение:

Графики линейных функций параллельны, если угловые коэффициенты(они же тангенсы углов наклона прямых, заданных данными функциями к оси абсцисс) этих функций равны а свободные члены отличаются. Если при равных угловых коэффициентах свободные члены равны, то прямые совпадают. Таким образом искомая функция примет вид у=7х+b. Однако по условию график искомой функции должен проходить через начало координат О(0;0). Подставим эти значения в функцию и найдем свободный член b. 0=0×х+b. Отсюда b=0. Следовательно искомая функция у=7х.

0,0(0 оценок)

Ответ:

Денисс2017

10.01.2023 22:56

$63^{72}; \hspace{2mm} 3^{143}*49^{36}; \hspace{2mm} 3^{143}*7^{71}$

Объяснение:

Для начала представим все многочлены в виде произведений простых чисел.

$3^{143}*49^{36} = 3^{143}*(7^2)^{36}=3^{143}*7^{36*2}=3^{143}*7^{72}\\63^{72}=(9*7)^{72}=9^{72}*7^{72}=(3^2)^{72}*7^{72}=3^{72*2}*7^{72}=3^{144}*7^{72}$

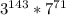А $3^{143}*7^{71}$ так и останется.

Заметим, что у всех трёх произведений одинаковые основания у множетелей: 3 и 7. Это даёт нам возможность сравнивать показатели степеней множителей.

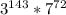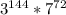Сравним $3^{143}*7^{72}$ и $3^{144}*7^{72}$ . Показатели степени 7 у обоих произведений одинаковы, а вот степень тройки справа на один больше, чем слева. Поэтому правое выражение больше левого.

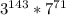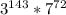Сравним $3^{143}*7^{71}$ и $3^{143}*7^{72}$ . Показатели степени 3 у обоих произведений одинаковы, а вот степень семёрки справа на один больше, чем слева. Поэтому правое выражение больше левого.

Получаем следующий порядок:

$3^{144}*7^{72} 3^{143}*7^{72}3^{143}*7^{71}$