Число делится на 55 если оно делится и на 5 и на 11. По признаку делимости на 5, число делится на 5 тогда, когда его последняя цифра 0 или 5, но так как если последняя цифра будет 0, то произведение цифр пятизначных чисел будет 0, поэтому последняя цифра будет 5.
Для удобства назовем наше число abcde, где каждая буква обозначает конкретный разряд числа: a – десятки тысяч, b – тысячи, c – сотни, d – десятки и e – единицы.
Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:
По условию задачи: . Возможные значения произведения пятизначного числа : 55, 60, 65, 70 и разложим каждое число на простые множители
Четыре последовательных натуральных числа таковы , что произведение двух меньших из них чисел на 78 меньше ,чем произведение больших чисел. Найдите наименьшее из этих чисел.
Решение.
Пусть х - первое число, оно же является наименьшим;
(х+1) - второе число;
(х+2) - третье число;
(х+3) - четвертое число, тогда
х·(х+1) - это произведение двух меньших из данных чисел, а
(х+2)·(х+3) - это произведение двух больших из данных чисел.
Число делится на 55 если оно делится и на 5 и на 11. По признаку делимости на 5, число делится на 5 тогда, когда его последняя цифра 0 или 5, но так как если последняя цифра будет 0, то произведение цифр пятизначных чисел будет 0, поэтому последняя цифра будет 5.
Для удобства назовем наше число abcde, где каждая буква обозначает конкретный разряд числа: a – десятки тысяч, b – тысячи, c – сотни, d – десятки и e – единицы.
Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:
По условию задачи: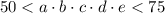
. Возможные значения произведения пятизначного числа : 55, 60, 65, 70 и разложим каждое число на простые множители
55 = 5 * 11
60 = 2 * 2 * 3 * 5
65 = 5 * 13
70 = 2 * 5 * 7
Перебираем возможные варианты составить числа и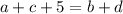
6, 5, 2, 1, 1 разбить никак
5, 4, 3, 1, 1: 5 + 1 + 1 = 4 + 3; ⇒ 14135, 13145
5, 3, 2, 2, 1 разбить никак
7, 5, 2, 1, 1: 5 + 2 + 1 = 7 + 1; ⇒ 27115, 21175, 17215, 11275
Отсюда наименьшее 11 275;
ответ: 11 275.
Четыре последовательных натуральных числа таковы , что произведение двух меньших из них чисел на 78 меньше ,чем произведение больших чисел. Найдите наименьшее из этих чисел.
Решение.
Пусть х - первое число, оно же является наименьшим;
(х+1) - второе число;
(х+2) - третье число;
(х+3) - четвертое число, тогда
х·(х+1) - это произведение двух меньших из данных чисел, а
(х+2)·(х+3) - это произведение двух больших из данных чисел.
По условию
х·(х+1) < (х+2)·(х+3) на 78
получаем уравнение:
(х+2)·(х+3) = х·(х+1) + 78 (ОДЗ; x∈N;)
x²+2x+3x+6 = x²+x+78
4x = 72
x = 72 : 4
x = 18
Получим четыре числа: 18; 19; 20; 21 из них
18 - является наименьшим.
ответ: 18.