Найдем производную функции f(x) по x:
Нам необходимо найти такие значения x, которые удовлетворяют условию:
или отсюда
откуда или
Из последнего уравнения
Итак, производная функции f(x) равна нулю в следующих точках:
f(x)=x^5+20x^2
f'(x)=0
f'(x)=5x^4+40x
5x^4+40x=0
5x(x^3+8)=0
5x=0 или х^3+8=0
x=0 x^3=-8
x=-2
Найдем производную функции f(x) по x:
Нам необходимо найти такие значения x, которые удовлетворяют условию:
откуда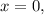 или
или 
Из последнего уравнения
Итак, производная функции f(x) равна нулю в следующих точках:
f(x)=x^5+20x^2
f'(x)=0
f'(x)=5x^4+40x
5x^4+40x=0
5x(x^3+8)=0
5x=0 или х^3+8=0
x=0 x^3=-8
x=-2