2. Найти нули производной: для этого приравнять производную к нулю и решить уравнение.
3. Построить числовую ось, отметить найденные точки и определить знаки производной на полученных интервалах.
1.
2.
3. На рисунке.
Как определены знаки на интервалах: берем произвольную точку из одного из интервалов, например на среднем, который от -4 до 2. На этом интервале лежит, например число 0. его и возьмем. Подставим в производную:
-24 < 0, значит на этом интервале функция убывает.
Такую же операцию проделываем и для двух других интервалов
Максимум - это точка в которой знак + меняется на знак -
-4
Объяснение:
Такие задачи решаем по схеме:
1. Найти производную функции.
2. Найти нули производной: для этого приравнять производную к нулю и решить уравнение.
3. Построить числовую ось, отметить найденные точки и определить знаки производной на полученных интервалах.
1.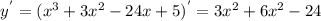
2.
3. На рисунке.
Как определены знаки на интервалах: берем произвольную точку из одного из интервалов, например на среднем, который от -4 до 2. На этом интервале лежит, например число 0. его и возьмем. Подставим в производную:
-24 < 0, значит на этом интервале функция убывает.
Такую же операцию проделываем и для двух других интервалов
Максимум - это точка в которой знак + меняется на знак -
Вывод: точка максимума равна -4