Под знаком корня стоит квадратичная функция f (x) = 4 - 4x - x²
Графиком этой функции является парабола с ветками, направленными вниз. Максимальное значение эта функция достигает в точке вершины параболы, координаты которой вычисляются по формулам
Так как 8 > 0, значит, точка x₀ принадлежит области определения функции , которая достигает своего максимального значения в точке x₀ = -2
Под знаком корня стоит квадратичная функция f (x) = 4 - 4x - x²
Графиком этой функции является парабола с ветками, направленными вниз. Максимальное значение эта функция достигает в точке вершины параболы, координаты которой вычисляются по формулам
Так как 8 > 0, значит, точка x₀ принадлежит области определения функции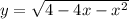 , которая достигает своего максимального значения в точке x₀ = -2
, которая достигает своего максимального значения в точке x₀ = -2
Точка максимума функции x = -2