Ищем точку минимума функции: .
Для этого сначала найдем производную этой функции:
Приравняем ее к нулю:
(При этом )
Дальше определяем знаки производной на числовой прямой:
+++++++++++ [-20] --------------- (0) --------------- [20] +++++++++
Как видим, точки экстремума - это и .
Но точкой минимума является именно вторая точка, так как при переходе через эту точку знак меняется с "-" на "+".
В ней значение функции равно .
Задача решена!
Ищем точку минимума функции: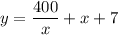 .
.
Для этого сначала найдем производную этой функции:
Приравняем ее к нулю:
(При этом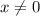 )
)
Дальше определяем знаки производной на числовой прямой:
+++++++++++ [-20] --------------- (0) --------------- [20] +++++++++
Как видим, точки экстремума - это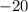 и
и 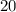 .
.
Но точкой минимума является именно вторая точка, так как при переходе через эту точку знак меняется с "-" на "+".
В ней значение функции равно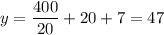 .
.
Задача решена!
ответ: 20.