Найдите удвоенное произведение всех корней уравнения ​

Домножим обе части уравнения на :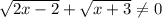

Первые две скобки можно раскрыть по формуле разности квадратов:

x = 5 – корень последнего полученного уравнения. Поищем другие корни, при x ≠ 5 на x - 5 можно сократить:

Итак, возможные корни уравнения – x = 5 и x = 5.5. Проверкой убеждаемся, что при подстановке каждого из этих значений в исходное уравнение получается верное равенство, так что в ответ пойдет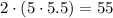

ответ. 55