Найдём ординату точки касания:
.
Находим производную:
y'=(x)'()+x('=+x(4)=+4x.
Находим значение производной в точне x=1:
f'(1)= + 4= 5
Теперь составим уравнение касательной:
y-=5(x-1) или y=(5x-4)
Найдём ординату точки касания:
Находим производную:
y'=(x)'(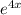 )+x(
)+x(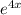 '=
'=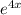 +x(4
+x(4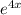 )=
)=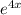 +4x
+4x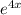 .
.
Находим значение производной в точне x=1:
f'(1)=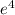 + 4
+ 4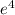 = 5
= 5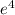
Теперь составим уравнение касательной:
y-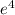 =5
=5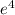 (x-1) или y=
(x-1) или y=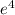 (5x-4)
(5x-4)
у=f(x0)+(f'(x0))(x-x0) ... (*)
найдём производную:
f'(x)=(x)'e^4x+x(e^4x)'=e^4x+4xe^4x.
f(1)=e⁴.
f'(1)=e⁴+4e⁴=5e⁴.
подставим полученные значения в формулу(*) :
у=е⁴+5е⁴(х-1).