3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.
8)
ответ: нет, не является, потому что должно быть натуральным числом.
9)
Наибольшее натуральное , удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
Второе решение не подходит, поскольку должно быть натуральным числом.
Воспользуемся формулой "сумма синусов равна удвоенному произведению синуса полусуммы на косинус полуразности":
2sin ((x+y)/2)cos ((x-y)/2)= - √2;
из первого уравнения ⇒sin((x+y)/2)=sin (π/2)=1, поэтому второе уравнение превращается в
sin((x-y)/2)=-√2/2; (x-y)/2=-π/4+2πn или (x-y)/2=-3π/4+2πk; x-y=-π/2+4πn или x-y=-3π/2+4πk. Чтобы получить ответ, сложим первое уравнение с получившимися и результат разделим на 2 (найдем x), а затем вычтем из первого получившиеся и результат разделим на 2 (найдем y).
x=π/4+2πn или x=-π/4+2πk; y=3π/4-2πn или y= 5π/4-2πk
ответ: (π/4+2πn; 3π/4-2πn); (-π/4+2πk; 5π/4-2πk); n, k∈Z
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.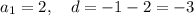
8)
ответ: нет, не является, потому что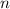 должно быть натуральным числом.
должно быть натуральным числом.
9)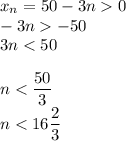
Наибольшее натуральное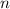 , удовлетворяющее этому неравенству, — это 16.
, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
Второе решение не подходит, поскольку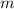 должно быть натуральным числом.
должно быть натуральным числом.
ответ: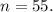
2sin ((x+y)/2)cos ((x-y)/2)= - √2;
из первого уравнения ⇒sin((x+y)/2)=sin (π/2)=1, поэтому второе уравнение превращается в
sin((x-y)/2)=-√2/2;
(x-y)/2=-π/4+2πn или (x-y)/2=-3π/4+2πk;
x-y=-π/2+4πn или x-y=-3π/2+4πk. Чтобы получить ответ, сложим первое уравнение с получившимися и результат разделим на 2 (найдем x), а затем вычтем из первого получившиеся и результат разделим на 2 (найдем y).
x=π/4+2πn или x=-π/4+2πk;
y=3π/4-2πn или y= 5π/4-2πk
ответ: (π/4+2πn; 3π/4-2πn); (-π/4+2πk; 5π/4-2πk); n, k∈Z