Найдите вершину и ось параболы заданной функцией и постройте эту параболу

1. 5(2a+1)-3=10a+5-3=10a-2=2(5a-1)

2. 18a^3+6a^2=6a^2(3a+1)

3.  (здесь степени съезжают, там будет 3^13 и так далее)

4. (x-6)^2-2x(-3x-6)=x^2-12x+36+6x^2+12x=7x^2+36

5. 5x+2(3-4x)=2x+21

5x+6-8x=2x+21

-3x+6=2x+21

-3x-2x=21-6

-5x=15

x=-3

6. a^2-ab-4a+4b=a(a-b)-4(a-b)=(a-b)(a-4)

7. Основание = x

Треугольник равнобедренный по условию, тогда боковая сторона = x-8

Периметр - сумма длин всех сторон, тогда x+2(x-8)=44

x+2x-16=44

3x=44+16

3x=60

x=20

Основание = 20 см

боковые стороны = 20-8=12 см

Объяснение:

ответ: 10 часов - был в пути велосипедист, выехавший из пункта А;

            15 часов - был в пути велосипедист, выехавший из пункта В.

Объяснение:

Пусть х часов с момента отправления до момента встречи велосипедистов.

Тогда 1-ый велосипедист, выехавший из пункта А был в пути (х + 4) часов, а 2-ой велосипедист, выехавший из пункта В, был в пути (х + 9) часов. Если принять длину пути за 1, то скорость 1-ого велосипедиста равна:    .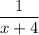

Скорость 2-ого велосипедиста равна:    .

Скорость сближения равна: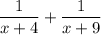      или   .

6 + 4 = 10 (ч) - был в пути велосипедист, выехавший из пункта А.

6 + 9 = 15 (ч) - был в пути велосипедист, выехавший из пункта В.