В приведенном квадратном уравнении , по теореме Виета, .
В вашем примере p=3+2a, q=2a+1. Подставив эти значения в формулу, получим:
.
После приведения подобных членов получим .
График этой функции - парабола с ветвями, направленными вверх. Значит, наименьшее значение эта функция приобретает в вершине параболы, абсцисса которой равна -1.
а=-1.
В приведенном квадратном уравнении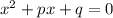 , по теореме Виета,
, по теореме Виета, 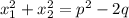 .
.
В вашем примере p=3+2a, q=2a+1. Подставив эти значения в формулу, получим:
После приведения подобных членов получим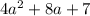 .
.
График этой функции - парабола с ветвями, направленными вверх. Значит, наименьшее значение эта функция приобретает в вершине параболы, абсцисса которой равна -1.