найдите значение произведения в функции f(x) в точке Хо​

1.

Приравниваем обе части

х-1=-х+3

2х=3+1=4

х=2

Подставляем в 1-ре уравнение

у=2-1=1

ответ: (2,1)

2.

Выразим 4а из 1-ого уравнения

4а=2+6b

Подставляем во 2-ое

2+6b+2b=3

8b=1

b=1/8

Ищем а:

2а-3*(1/8)=1

2a=1+3/8=11/8

a=11/16

ответ (11/16,1/8)

4.

Пусть х - количество монет номиналом по 2 рубля, а у количество монет носиком по 5 рублей

Составляем систему:

х+у=18

2х+5у=97

Из 1-ого вырадаем х:

х=18-у

Подставляем во 2-ое

2(18-у)+5у=97

36-2у+5у=97

3у=97-36=61

у=61/3

х=18-61/3=-7/3

Объяснение:

Кажется в 4 номере неправильные цифры, т. к. получилось, что количество монет, дробное или отрицательное число

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .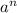

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .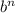

Рассмотрим многочлен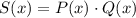 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :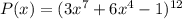

- степень определяется выражением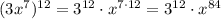 , то есть степень равна 84

- свободный член равен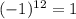

Для многочлена :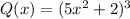

- степень определяется выражением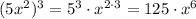 , то есть степень равна 6

- свободный член равен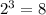

Наконец, для многочлена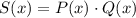 получим:

- степень определяется выражением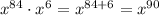 , то есть степень равна 90

- свободный член равен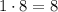

Сумма степени и свободного члена многочлена :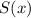

ответ: 98