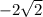f(x) = 6cosx + 2sinx, x₀ = π/4
f'(x) = -6sinx + 2cosx
f'(x₀) = f'(π/4) = -6sin(π/4) + 2cos(π/4) = -6 · √2/2 + 2 · √2/2 = -3√2 + √2 = -2√2
-2√2
Найдём производную f'(x)
Подставим в f'(x) x = π/4
ответ:
f(x) = 6cosx + 2sinx, x₀ = π/4
f'(x) = -6sinx + 2cosx
f'(x₀) = f'(π/4) = -6sin(π/4) + 2cos(π/4) = -6 · √2/2 + 2 · √2/2 = -3√2 + √2 = -2√2
ответ-2√2
Найдём производную f'(x)
Подставим в f'(x) x = π/4
ответ: