25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е. .
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е. .
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
Найдем точку при x=−2
Заменим в выражении переменную x на −2
f(−2)=2(−2)−(−2)^3
Упростим результат.
f(−2)=−4−(−2)^3
Возведем −2 в степень 3
f(−2)=−4+8
f(−2)=4
Итоговым ответом является 4
y=4
Найдем точку при x=−1
Заменим в выражении переменную x на −1
f(−1)=2(−1)−(−1)^3
f(−1)=−2+1
f(−1)=−1
Итоговым ответом является −1
y=−1
Найдем точку при x=0
Заменим в выражении переменную x на 0
f(0)=2(0)−(0)^3
f(0)=0−0^3
f(0)=0
Итоговым ответом является 0
y=0
Найдем точку при x=1
f(1)=2(1)−(1)^3
f(1)=2-1*1
f(1)=1
Итоговым ответом является 1
y=1
Найдем точку при x= 2
f(2)=2(2)−(2)^3
f(2)=−4−(2)^3
Возведем 3 в степень 3
f(2)=4-8
f(2)=-4
Итоговым ответом является -4
y=-4
График кубической функции можно построить, учитывая поведение функции и используя данные точки.
x y
-2 4
-1 -1
0 0
1 1
2 -4
График кубической функции можно построить, учитывая поведение функции и используя выбранные точки. Возрастает влево и убывает вправо
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е.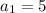 .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е.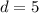 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
Найдем точку при x=−2
Заменим в выражении переменную x на −2
f(−2)=2(−2)−(−2)^3
Упростим результат.
f(−2)=−4−(−2)^3
Возведем −2 в степень 3
f(−2)=−4+8
f(−2)=−4+8
f(−2)=4
Итоговым ответом является 4
y=4
Найдем точку при x=−1
Заменим в выражении переменную x на −1
f(−1)=2(−1)−(−1)^3
Упростим результат.
f(−1)=−2+1
f(−1)=−1
Итоговым ответом является −1
y=−1
Найдем точку при x=0
Заменим в выражении переменную x на 0
f(0)=2(0)−(0)^3
f(0)=0−0^3
f(0)=0
Итоговым ответом является 0
y=0
Найдем точку при x=1
f(1)=2(1)−(1)^3
Упростим результат.
f(1)=2-1*1
f(1)=1
Итоговым ответом является 1
y=1
Найдем точку при x= 2
f(2)=2(2)−(2)^3
Упростим результат.
f(2)=−4−(2)^3
Возведем 3 в степень 3
f(2)=4-8
f(2)=-4
Итоговым ответом является -4
y=-4
График кубической функции можно построить, учитывая поведение функции и используя данные точки.
x y
-2 4
-1 -1
0 0
1 1
2 -4
График кубической функции можно построить, учитывая поведение функции и используя выбранные точки. Возрастает влево и убывает вправо
x y
-2 4
-1 -1
0 0
1 1
2 -4