НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ sin a ctg a ЗНАЯ ЧТО cos a = 8/17 И 3P/2 МЕНЬШЕ АЛЬФА МЕНЬШЕ 2 ПИ

Показать ответ

Ответ:

Голубоглазый234

15.06.2022 10:46

Осминин_Кирилл

Ученик 6в класса

view_quilt

Лента

alarm

Расписание

date_range

Календарь

subject

Выписка оценок

equalizer

Табель

history_edu

Все задания

NEW

help

settings

Настройки

Версия 2.1.2

(20120)

Первая четверть

help_outline

История Казахстана

8/10

10/10

8/10

1/10

10/10

1/10

График оценок

star

16/17

star

11/25

help_outline

Русский язык

5/10

6/10

5/10

6/10

5/10

6/10

5/10

График оценок

star

9/13

star

9/13

Русская литература

6/10

5/10

6/10

5/10

6/10

5/10

6/10

График оценок

star

9/13

star

9/13

help_outline

Математика

5/10

4/10

5/10

4/10

5/10

7/10

1/10

3/10

5/10

График оценок

star

7/15

star

14/20

help_outline

Всемирная история

6/10

10/10

1/10

График оценок

star

17/20

Иностранный язык

6/10

10/10

6/10

5/10

6/10

5/10

График оценок

star

5/10

star

7/13

Классный час

Оценки не выставлены

Музыка

Оценки не выставлены

help_outline

Естествознание

8/10

7/10

5/10

8/10

7/10

5/10

10/10

7/10

5/10

7/10

10/10

1/10

График оценок

star

10/15

star

20/20

help_outline

Информатика

8/10

График оценок

star

11/13

help_outline

Казахский язык и литература

8/10

7/10

8/10

7/10

1/10

7/10

6/10

График оценок

star

11/13

star

7/13

Физическая культура

Оценки не выставлены

Художественный труд

Оценки не выставлены

Самопознание

Оценки не выставлены

0,0(0 оценок)

Ответ:

рузик83

10.05.2020 21:02

Объяснение:

Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:

$\frac{1}{12} (2n^6+6n^5+5n^4-n^2)=\frac{n^2(2n^4+6n^3+5n^2-1)}{12} =\frac{n^2(2n^4+2n^3+4n^3+4n^2+n^2+n-n-1)}{12} =\frac{n^2(2n^3(n+1)+4n^2(n+1)+n(n+1)-(n+1))}{12} =\frac{n^2(n+1)(2n^3+4n^2+n-1)}{12} =\\=\frac{n^2(n+1)(2n^3+2n^2+2n^2+2n-n-1)}{12} =\frac{n^2(n+1)(2n^2(n+1)+2n(n+1)-(n+1))}{12}=\frac{n^2(n+1)^2(2n^2+2n-1)}{12}$ А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.

Теперь предположим что равенство верно для n=k:

$1^5+2^5+...+k^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}$

Прибавив к обеим частям равенства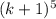 (k+1)^5 получим:

$1^5+2^5+...+k^5+(k+1)^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5$

Займёмся преобразованием правой части этого равенства:

$\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5=(k+1)^2\bigg(\frac{k^2(2k^2+2k-1)}{12} +(k+1)^3\bigg)=\\=\frac{(k+1)^2}{12} \big(k^2(2k^2+2k-1)+12(k^3+3k^2+3k+1)\big)=\\=\frac{(k+1)^2}{12}\big(2k^4+14k^3+35k^2+36k+12\big)=\frac{(k+1)^2(2k^4+4k^3+10k^3+20k^2+15k^2+30k+6k+12)}{12}=\\=\frac{(k+1)^2(2k^3(k+2)+10k^2(k+2)+15k(k+2)+6(k+2))}{12}=\frac{(k+1)^2(k+2)(2k^3+10k^2+15k+6)}{12}=\\=\frac{(k+1)^2(k+2)(2k^3+4k^2+6k^2+12k+3k+6)}{12}=\frac{(k+1)^2(k+2)(2k^2(k+2)+6k(k+2)+3(k+2))}{12}=$ $=\frac{(k+1)^2(k+2)^2(2k^2+6k+3)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2k+1)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$ Таким образом

$1^5+2^5+...+k^5+(k+1)^5=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$

То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.

Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.

0,0(0 оценок)

Популярные вопросы: Алгебра