Известно, что у функции главный период функции равен . Что же будет с функцией, где аргумент в три раза меньше?
Например, , максимума, то есть единицы, достигает при
, а у , надо чтобы , то есть в три раза больше. То есть уменьшая аргумент, мы растягиваем функцию по оси ОХ. В данном случае растягиваем по ОХ в 3 раза. А значит, и период вырастет в три раза. Так как период равен , то для нашей функции он будет равен
Известно, что у функции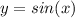 главный период функции равен
главный период функции равен 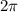 . Что же будет с функцией, где аргумент в три раза меньше?
. Что же будет с функцией, где аргумент в три раза меньше?
Например,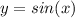 , максимума, то есть единицы, достигает при
, максимума, то есть единицы, достигает при
ответ: 6
P.S. для наглядности графики на картинке