1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли
Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.
Здесь ситуация аналогичная и ответ: нет.
2. Решаем уравнения
Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ:
Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.
В порядке убывания ответ будет такой:
3. Просто раскладываем:
4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):
Отношение массы золота к массе серебра для 1-го и 2-го сплава соответственно.
Выразим золото в обоих случаях, так как оно через умножение будет (это удобнее)
Что такое масса сплава
Для конкретных сплавов это:
Далее составляется новый сплав, который составляется из первого и второго сплава, но возьмутся части от каждого. Пусть эти доли будут равны для первого и второго сплава соответственно.
Общая масса нового сплава будет равна:
Причем суммарная масса золота здесь будет
Первое слагаемое - масса золота в новом сплаве из первого сплава, второе слагаемое - масса золота в новом сплаве из второго сплава.
И вот тут применяем условие, что эти два слагаемых равны, то есть
Вспомним, какие будут массы первого и второго сплава в новом сплаве и найдем их отношение.
Из заданных можно лишь сказать, что оба сомножителя будут больше единицы, так что и все произведение будет больше единицы, то есть масса первого сплава должна быть больше.
UPD. Дорешивал я уже задачу, где массы золота в новом сплаве равны (изначально недопонял условие)
Но нестрашно. Тоже полезно. Теперь дорешаем нашу задачу. В ней равны массы золота и серебра в новом сплаве.
Общая масса золота в новом сплаве это
Общая масса серебра в новом сплаве это
И известно, что эти массы равны. Логика та же: приравнять, выразить и подставить.
Замечательно. Только для удобства обозначим
Вспоминаем, что
А вот здесь как раз вполне можно использовать знание, что и поменять знаки одновременно в скобках с вычитанием как в числителе, так и в знаменателе и тогда
1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли
Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.
Здесь ситуация аналогичная и ответ: нет.
2. Решаем уравнения
Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ: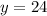
Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.
В порядке убывания ответ будет такой:
3. Просто раскладываем:
4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):
5. Тут уже даже первое действие дано
Распишу, как я вижу эту задачу
Пусть масса золота будет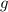 , серебра
, серебра 
Отношение массы золота к массе серебра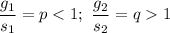 для 1-го и 2-го сплава соответственно.
для 1-го и 2-го сплава соответственно.
Выразим золото в обоих случаях, так как оно через умножение будет (это удобнее)
Что такое масса сплава
Для конкретных сплавов это:
Далее составляется новый сплав, который составляется из первого и второго сплава, но возьмутся части от каждого. Пусть эти доли будут равны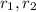 для первого и второго сплава соответственно.
для первого и второго сплава соответственно.
Общая масса нового сплава будет равна:
Причем суммарная масса золота здесь будет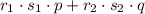
Первое слагаемое - масса золота в новом сплаве из первого сплава, второе слагаемое - масса золота в новом сплаве из второго сплава.
И вот тут применяем условие, что эти два слагаемых равны, то есть
Вспомним, какие будут массы первого и второго сплава в новом сплаве и найдем их отношение.
Из заданных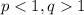 можно лишь сказать, что оба сомножителя будут больше единицы, так что и все произведение будет больше единицы, то есть масса первого сплава должна быть больше.
можно лишь сказать, что оба сомножителя будут больше единицы, так что и все произведение будет больше единицы, то есть масса первого сплава должна быть больше.
UPD. Дорешивал я уже задачу, где массы золота в новом сплаве равны (изначально недопонял условие)
Но нестрашно. Тоже полезно. Теперь дорешаем нашу задачу. В ней равны массы золота и серебра в новом сплаве.
Общая масса золота в новом сплаве это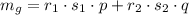
Общая масса серебра в новом сплаве это
И известно, что эти массы равны. Логика та же: приравнять, выразить и подставить.
Замечательно. Только для удобства обозначим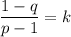
Вспоминаем, что
А вот здесь как раз вполне можно использовать знание, что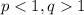 и поменять знаки одновременно в скобках с вычитанием как в числителе, так и в знаменателе и тогда
и поменять знаки одновременно в скобках с вычитанием как в числителе, так и в знаменателе и тогда
Как-то так.