1) При одновременном броске двух игральных кубиков - 6 × 6 = 36 вариантов выпадения очков. И только в одном случае сумма очков будет меньше 3, это когда на обоих кубиках выпадет по 1 очку. Значит, вероятность равна 1/36. В ответ пишем обратную величину: 36.
2) Стрелок попадает в мишень с вероятностью 0,7 и не попадает с вероятностью 0,3. Значит, после трёх выстрелов вероятность ни разу не попасть равна 0,3 × 0,3 × 0,3 = 0,027. Тогда вероятность того, что стрелок попадёт с трёх раз хотя бы один раз (это м.б. и 1, и 2, и 3 раза) равна: 1 - 0,027 = 0,973
2) Стрелок попадает в мишень с вероятностью 0,7 и не попадает с вероятностью 0,3. Значит, после трёх выстрелов вероятность ни разу не попасть равна 0,3 × 0,3 × 0,3 = 0,027.
Тогда вероятность того, что стрелок попадёт с трёх раз хотя бы один раз (это м.б. и 1, и 2, и 3 раза) равна:
1 - 0,027 = 0,973
прощения, но решение получилось слишком сложным :(
q - знаменатель геом. прогр.
d - сумма арифм. прогрессии
a - первый член ар. прогр.
b - первый член геом. прогр.
1) a+d+a+2d=2a+3d=12; также b+bq=b(1+q)=12; также bq+a+d=12
2) a+2d=bq
3) a+d=b
4) a+bq^2=14
из b(1+q)=12:
из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)
т.е.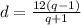
из a+bq^2=14 выразим a=14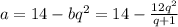
Подставим в 2a+3d=12 получим квадратное уравнение вида:
После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:
Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.
Отсюда b=8, a=12, d=-4
Получаем последовательность:
12 8 4 2