Раскроем скобки в правой части:
Два многочлена равны, если равны соответствующие коэффициенты при степенях. Получаем систему:
Старшие коэффициенты и свободные члены, очевидно, равны, поэтому в систему их не включаем.
Из первого условия получили, что , из второго уравнения найдем, что .
Эти значения удовлетворяют 3 и 4 уравнению.
Значит, равенство выполняется при A=1 и В=-8.
ответ: A=1; В=-8
Раскроем скобки в правой части:
Два многочлена равны, если равны соответствующие коэффициенты при степенях. Получаем систему:
Старшие коэффициенты и свободные члены, очевидно, равны, поэтому в систему их не включаем.
Из первого условия получили, что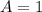
, из второго уравнения найдем, что 
.
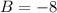Эти значения удовлетворяют 3 и 4 уравнению.
Значит, равенство выполняется при A=1 и В=-8.
ответ: A=1; В=-8