Найти cosx, если sinx=(-2√6)/5, x€(pi; 3pi/2)​

Рассмотрим указанный диапазон натуральных чисел как расширенный натуральный ряд (то есть такой, куда входит 0). Разобьём этот ряд на пары. Получим:

0;999999999

1;999999998

2;999999997

3;999999996

...и так далее.

Одно число (1000000000) останется без пары.

Из составленного понятно, что сумма цифр в одной паре равна: .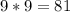

Так как мы разбили ряд на две равные части, количество пар будет равно:

Зная это, умножим сумму цифр в одной паре на количество пар и добавим 1, так как одно число у нас осталось без пары.

ответ: 40500000001

"-x-x²≥-11+1 как получается -2x²≥-10"

Одно из другого никак не получается, разные степени нельзя прибавить таким образом.

если решить обе задачки, то видно, что корни разные, лишнее док-во, что это разные выражения и друг из друга не получаются

1) -2x²≥-10;

x²≤5;

-√5≤x≤√5;

2)-x-x²≥-11+1;

-x²-x+10≥0;

D=1+4*10=41;

x₁=(1+√41)/-2=-0,5(√41+1);

x₂=(1-√41)/-2=0,5(√41-1);

   -                            +                          -

-0,5(√41+1)0,5(√41-1)

-0,5(√41+1)≤x≤0,5(√41-1);

3) вариант: 11-x≥(x+1)²;

11-x≥x²+2x+1;

-x²-2x-1+11-x≥0;

-x²-3x+10≥0;

D=9+4*10=49;

x₁=(3+7)-2=-5;

x₁=(3-7)-2=2;

   -          +          -

-52

-5≤x≤2;