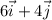Градиентом функции называется вектор вида:
Для его получения найдем частные производные функции:
Подставим в формулу градиента:
Вычислим значение градиента в точке М, то есть при и :
ответ:
Градиентом функции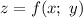 называется вектор вида:
называется вектор вида:
Для его получения найдем частные производные функции:
Подставим в формулу градиента:
Вычислим значение градиента в точке М, то есть при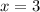 и
и 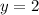 :
:
ответ: