А значит интервал сходимости
Исследуем на концах:
- сходится как обобщенный гармонический ряд с
Заметим, что ряд из модулей сходится (по доказанному ранее). А значит и ряд сходится
А тогда исходный ряд сходится на
А значит интервал сходимости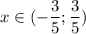
Исследуем на концах:
Заметим, что ряд из модулей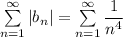 сходится (по доказанному ранее). А значит и ряд
сходится (по доказанному ранее). А значит и ряд 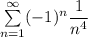 сходится
сходится
А тогда исходный ряд сходится на![\left[-\dfrac{3}{5};\dfrac{3}{5}\right]](/tpl/images/1432/1335/e77ae.png)