у>0 на интервале (-∞;2- ) и (2+ ;+∞)
у<0 на интервале (2- ; 2+ )
Объяснение:
1) Находим область определения функции.
Это квадратичная функция. График - парабола
Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Находим нули функции.
Чтобы найти нули функции нужно решить уравнение x²-4x+1=0, то есть найти те значения «икс», при которых функция обращается в ноль.
x²-4x+1 = 0
х₁ = 2- , х₂ = 2-
3) Откладываем все найденные точки на числовой оси:
___..___
2- 2+
В данном случае ветви параболы направлены вверх (т.к. коэффициент при х² больше 0), следовательно, на интервалах (-∞;2- ) и (2+ ;+∞)
функция будет положительна, а на интервале (2- ; 2+ ) - функция будет отрицательна.
у>0 на интервале (-∞;2-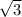 ) и (2+
) и (2+ 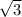 ;+∞)
;+∞)
у<0 на интервале (2-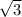 ; 2+
; 2+ 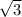 )
)
Объяснение:
1) Находим область определения функции.
Это квадратичная функция. График - парабола
Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Находим нули функции.
Чтобы найти нули функции нужно решить уравнение x²-4x+1=0, то есть найти те значения «икс», при которых функция обращается в ноль.
x²-4x+1 = 0
х₁ = 2-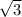 , х₂ = 2-
, х₂ = 2- 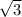
3) Откладываем все найденные точки на числовой оси:
___..___
2-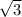 2+
2+ 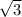
В данном случае ветви параболы направлены вверх (т.к. коэффициент при х² больше 0), следовательно, на интервалах (-∞;2-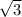 ) и (2+
) и (2+ 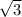 ;+∞)
;+∞)
функция будет положительна, а на интервале (2-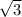 ; 2+
; 2+ 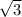 ) - функция будет отрицательна.
) - функция будет отрицательна.