Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
Qocharian
22.03.2020 03:19 •
Алгебра
Найти наибольшее целое число удовлетворяющие неравенству f'(x)<0 , если f(x)=x³-3x²-6x
Показать ответ
Ответ:
AnnyKat
03.09.2021 23:20
2
Объяснение:
0,0
(0 оценок)
Ответ:
ИльяМамедов2
03.09.2021 23:20
1-
<x<1+
Объяснение:
f'(x)=3x^2+6x-6<0
f'(x)=x^2+2x-2<0
x1=1-
x2=1+
0,0
(0 оценок)
Популярные вопросы: Алгебра
мαрия
19.07.2022 04:22
Да казать тождество (a+b)^2-2ab+a^2-b^2=a*2a...
09kok90
19.07.2022 04:22
Решите систему уравнений 1) 3x -y =3 2) 5x + 2y =16...
IvanShadow
19.07.2022 04:22
Решите 55 . постройте графики функций в одной системе координат. у = х^2 у = х^2 + 2 у = х^2 - 5 у = (х-4)^2 у = (х+3)^2...
kati456miks
19.07.2022 04:22
Найдите количество членов арифметической прогрессии (an) , еслиa1=6 , an=-279 , d= -3 ....
thenotoriioussmma
13.06.2020 09:35
Варифметической прогрессии 7 член равен 12. найдите сумму первых 13 ее членов...
olesay12345
13.06.2020 09:35
Вычислите сумму первых 7 членов арифметических прогрессии, в которых a1 = 6; d = 1 2/3...
ЕваКимСокДжин
13.06.2020 09:35
Варифметической прогрессии a1 = -4; d = 0,4; an = -2. найдите количество членов n...
marsik261
13.06.2020 09:35
Найдите разность и 4 член заданной арифметической прогрессии: 3/15 ; 8/15 ; 13/15...
vadim2556
13.06.2020 09:35
Представьте многочлен в виде произведения. укажите хотя бы одно значение а, при котором произведение будет равно нулю: а) 10а - 5а^2; б) а^2 - 25 ....
Angelina07111
28.04.2022 00:50
Стальная деталь машины весит 780 г определите ее объемы...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
2
Объяснение:
1-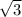 <x<1+
<x<1+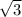
Объяснение:
f'(x)=3x^2+6x-6<0
f'(x)=x^2+2x-2<0
x1=1-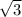
x2=1+