Преобразуем выражение следующим образом:
Воспользуемся формулой синуса двойного угла:
Зная, что синус принимает значения из отрезка от -1 до 1, оценим заданное выражение:
Значит, наименьшее значений функции равно , а наибольшее значение функции равно .
Преобразуем выражение следующим образом:
Воспользуемся формулой синуса двойного угла:
Зная, что синус принимает значения из отрезка от -1 до 1, оценим заданное выражение:
Значит, наименьшее значений функции равно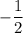 , а наибольшее значение функции равно
, а наибольшее значение функции равно  .
.