нам задана функция
для того чтобы упростить нашу работу обозначим и тогда получим простую квадратичную функцию
1. областью этой функции является вся область вещественных значений аргумента и отрезок [-3;2] принадлежит этой области.
2. Найдем производную функции
очевидно, что производная существует во всех точках отрезка [-3;2].
3. найдем стационарную точку для функции для чего приравняем производную к нулю
, но мы помним, что следовательно
4. и так стационарная точка совпадает с концом заданного отрезка, поэтому найдем значение функции только на его концах
получаем
maxy=y(2)=-11
miny=y(-3)=-148
нам задана функция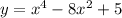
для того чтобы упростить нашу работу обозначим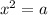 и тогда получим простую квадратичную функцию
и тогда получим простую квадратичную функцию 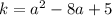
1. областью этой функции является вся область вещественных значений аргумента и отрезок [-3;2] принадлежит этой области.
2. Найдем производную функции
очевидно, что производная существует во всех точках отрезка [-3;2].
3. найдем стационарную точку для функции для чего приравняем производную к нулю
4. и так стационарная точка совпадает с концом заданного отрезка, поэтому найдем значение функции только на его концах
получаем
maxy=y(2)=-11
miny=y(-3)=-148