Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.
Тригонометрия возникла из пратических нужд человека. С ее можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.
Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вс разделом.
Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.
Выполнить построение графиков, взяв в качестве двух опорных точек случайное значение аргумента, посчитать значение функций. Таким образом отложить в системе координат две точки для каждого графика и соединить их проходящей через них прямой. Графики пересекутся, найти точку пересечения и записать ее координаты
Но этот метод не оптимален, так как получится значение в 2.9 см, что и мерить то будет неудобно. Можно его нарисовать, не повредит, но мы будем делать упор на 2-й путь
2-й
Приравняем функции, необходимо решить линейное уравнение, найдя значение аргумента x, которое будет равно для двух функций:
y = y
0.3x + 2 = x - 0.1
0.3x + 2.1 = x
x - 0.3x = 2.1
0.7x = 2.1
x = = 3
Подставим значение аргумента в любую из двух функций, чтобы найти значение y, наиболее удобной будет вторая:
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.
Тригонометрия возникла из пратических нужд человека. С ее можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.
Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вс разделом.
Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.
Да, пересекаются
Точка пересечения графиков - (3, 2.9)
Объяснение:
Найти точку пересечения можно двумя путями
1-й
Выполнить построение графиков, взяв в качестве двух опорных точек случайное значение аргумента, посчитать значение функций. Таким образом отложить в системе координат две точки для каждого графика и соединить их проходящей через них прямой. Графики пересекутся, найти точку пересечения и записать ее координаты
Но этот метод не оптимален, так как получится значение в 2.9 см, что и мерить то будет неудобно. Можно его нарисовать, не повредит, но мы будем делать упор на 2-й путь
2-й
Приравняем функции, необходимо решить линейное уравнение, найдя значение аргумента x, которое будет равно для двух функций:
y = y
0.3x + 2 = x - 0.1
0.3x + 2.1 = x
x - 0.3x = 2.1
0.7x = 2.1
x =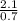 = 3
= 3
Подставим значение аргумента в любую из двух функций, чтобы найти значение y, наиболее удобной будет вторая:
y = x - 0.1
y = 3 - 0.1
y = 2.9
Или:
y = 0.3x +2
y = 0.3 * 3 + 2 = 0.9 + 2
y = 2.9
Что и требовалось доказать