Пусть . Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра , при котором система имеет хотя бы одно решение. Первое уравнение задает прямую в , а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая , мы поднимаем прямую, значит, максимальному соответствует случай касания прямой и окружности.
. По теореме Пифагора найдем . При этом, очевидно: , подставляем: .
Пусть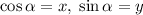 . Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра
. Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра  , при котором система
, при котором система 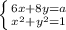 имеет хотя бы одно решение. Первое уравнение задает прямую
имеет хотя бы одно решение. Первое уравнение задает прямую 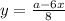 в
в 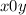 , а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая
, а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая  , мы поднимаем прямую, значит, максимальному
, мы поднимаем прямую, значит, максимальному  соответствует случай касания прямой и окружности.
соответствует случай касания прямой и окружности.
ответ: 10