По условию, нас интересуют положительные корни:
Значит, при формула дает положительные корни, причем чем меньше значение , тем меньше значение корня.
Минимальное целое число, удовлетворяющее условию : .
Находим наименьшей положительный корень:
ответ: 2п/3
По условию, нас интересуют положительные корни:
Значит, при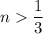 формула дает положительные корни, причем чем меньше значение
формула дает положительные корни, причем чем меньше значение 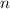 , тем меньше значение корня.
, тем меньше значение корня.
Минимальное целое число, удовлетворяющее условию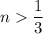 :
: 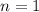 .
.
Находим наименьшей положительный корень:
ответ: 2п/3