Как известно, если есть две периодические функции с периодами T1 и T2 , то периодом их суммы, разности и частного является число T, кратное T1 и T2.
Период sinx = 2k, где k - целое число.
Период tgx = n, где n - целое число.
Наименьшим положительным периодом будет являться число 2, так как при k = 1 и n = 1, оно кратно обоим периодам.
Теперь проверим, что 2 действительно является периодом функции:
f(x) = f( x + T), f( x + 2) = sin(x + 2) + tg(x + 2) = sinx + tgx.
Как видно из вышенаписанного, число 2 действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
ответ: 2
Наименьший положительный период функции - это наименьшее положительное число T, являющееся периодом данной функции.
Рассмотрим наименьшие периоды каждого слагаемого.
Для sinx T₁=2π, для tgx T₂=π.
Период суммы - это наименьшее число, которое делится на Т₁ и Т₂.
Найти наименьший положительный период функции y=sinx+tgx T = 2π
Как известно, если есть две периодические функции с периодами T1 и T2 , то периодом их суммы, разности и частного является число T, кратное T1 и T2.
Период sinx = 2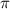 k, где k - целое число.
k, где k - целое число.
Период tgx =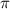 n, где n - целое число.
n, где n - целое число.
Наименьшим положительным периодом будет являться число 2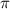 , так как при k = 1 и n = 1, оно кратно обоим периодам.
, так как при k = 1 и n = 1, оно кратно обоим периодам.
Теперь проверим, что 2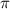 действительно является периодом функции:
действительно является периодом функции:
f(x) = f( x + T), f( x + 2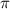 ) = sin(x + 2
) = sin(x + 2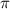 ) + tg(x + 2
) + tg(x + 2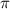 ) = sinx + tgx.
) = sinx + tgx.
Как видно из вышенаписанного, число 2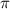 действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
ответ: 2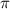
Наименьший положительный период функции - это наименьшее положительное число T, являющееся периодом данной функции.
Рассмотрим наименьшие периоды каждого слагаемого.
Для sinx T₁=2π, для tgx T₂=π.
Период суммы - это наименьшее число, которое делится на Т₁ и Т₂.
Найти наименьший положительный период функции y=sinx+tgx T = 2π